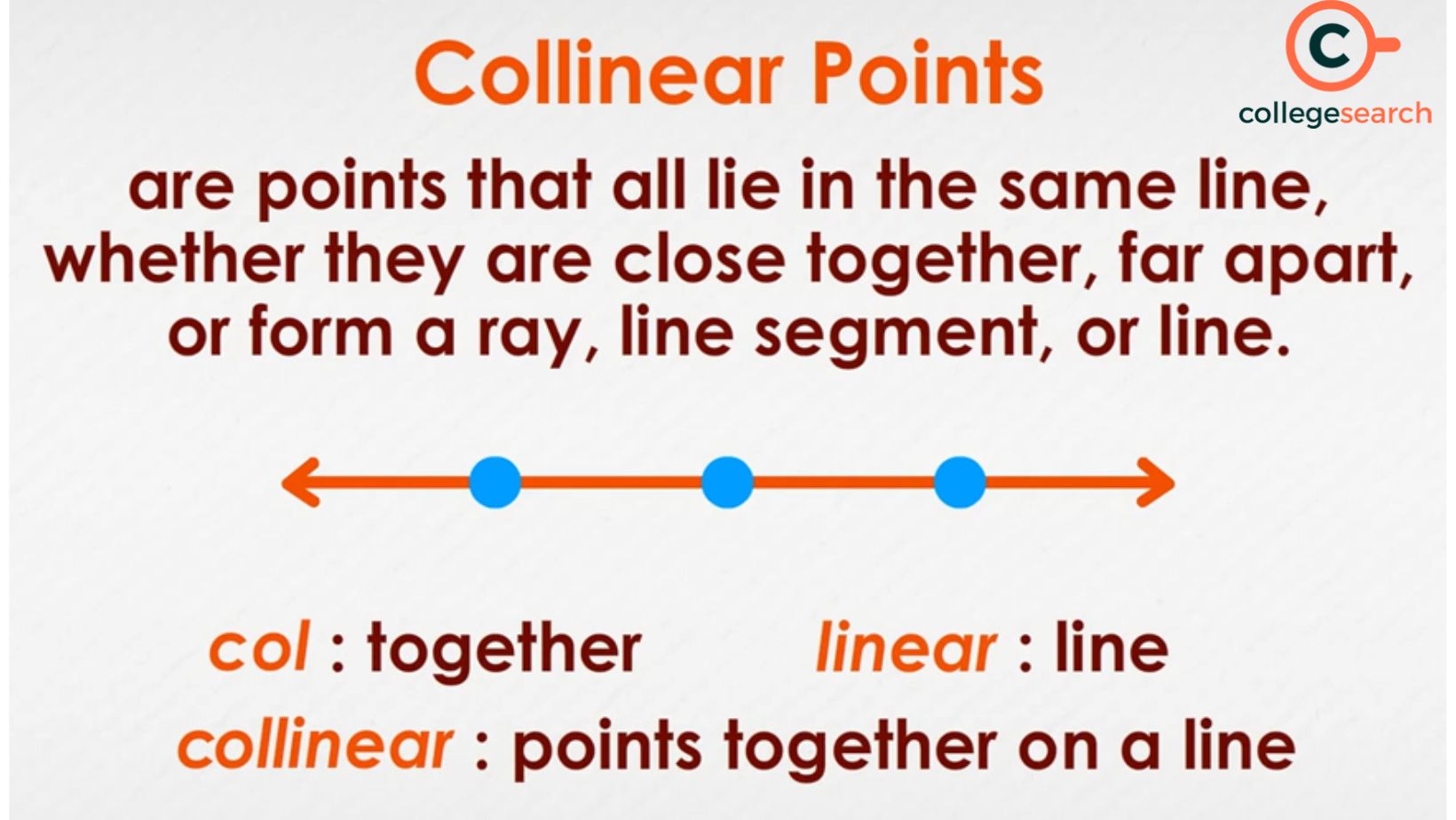
Three or more points on the same line are referred to as collinear points. The term "collinear" is a composite word comprised of the words "co," which refers to togetherness, and "linear," which denotes a line. On separate planes, collinear points may occur, but not on different lines. It is referred to as collinearity since the points are parallel. Points that do not lie on a straight line are referred to as non-collinear points.
What are Collinear Points?
The phrase "collinear is the combination word of two Latin terms, 'col' and 'linear'. 'Col' stands for together, while "linear" is for the line. As a result, collinear points are points that are connected by a single line. For Example: Many real-life examples of collinearity may be found, such as a group of students standing in a straight line, a row of apples stored close to each other, and so on.
More astonishingly, the term collinear has been employed for straightened items, which signifies something is "in a row" or "in a line."
Read more: Father of Mathematics and Who Invented Math?
Collinear Points Formula
There are several ways to tell if three points are parallel or not. The slope formula, the area of the triangle formula, and the distance formula are the three most often used formulae to determine whether two points are collinear or not. The following is the formula for collinear points-
Area of Triangle Formula
This approach makes use of the fact that three collinear points can never form a triangle. This indicates that no triangle can be formed if any three points are collinear. As a result, we validate the triangle's points by including them in the calculation for the triangle's area. These points will be regarded as collinear if the area is equal to 0. In other words, the triangle created by three collinear points will only be a line connecting the three points and will not have any area. The formula for a triangle's area, which is used to determine if two points are collinear. Triangle with the specified points (vertices) A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) is-

Distance Formula
We calculate the distance between the first and second points using the distance formula before calculating the distance between the second and third points. After that, we determine if the distance between the first and third points is equal to the total of these two distances. Only if the three points are collinear will this be achievable. We employ the distance formula to determine the separation between two places whose coordinates are known to us. The separation between two points A(x₁, y₁) and B(x₂, y₂) is-

Therefore, if there are three collinear points in positions A, B, and C, then AB + BC = CA will cause these points to be collinear.
Read more about the Unit of Distance.
Slope Formula
To get the slope of the lines that the three points under investigation create, we use the slope formula. The three points are collinear if the three slopes are equal. Three points X, Y, and Z, for instance, will only be collinear if the slope of line XY equals the slope of line YZ equals the slope of line XZ. We employ the slope formula to get the slope of the line connecting two locations.
A line connecting two points gradient P (x₁, y₁) and Q (x₂, y₂) is-

Read more about the Various Formulas of Math.
How to Determine that Two Points Are Collinear?
There are two ways to determine if the three points are parallel, and they are as follows-
- The area of the triangle approach is the alternative.
- The slope formula technique is one of them.
Applications of Collinear Points
Applications of collinear points in daily life include keeping a set of balls in a straight line or having pupils stand in a straight line during an assembly. Collinear points play a crucial role in resolving practical Euclidean geometry issues.
Read more about Difference Between Distance and Displacement.
Points to Remember
- Any triangle created by three collinear points will always have a surface area of zero.
- Collinear points are three or more points that are located on the same straight line.
- Non-linear points are those that are situated at non-linear angles so that a straight line cannot be drawn from them.
- There are three primary methods for determining whether or not points are collinear.
- When three points are parallel to one another, any two of those points' slopes will equal the slope created by the other two.

