Types of Number System: Definition, Conversion, Equations & Examples

Types of Number System Overview

Number systems play a crucial role in mathematics and are essential for computer understanding. They allow us to represent numbers in different forms and facilitate arithmetic calculations. Numbers, as mathematical values used for counting and measuring, can be categorized into various types, such as natural numbers, whole numbers, rational numbers, irrational numbers, and more. Similarly, there are different number systems, each with unique properties. These include the binary number system, the octal number system, the decimal number system, and the hexadecimal number system.

In this article, we will delve into the exploration of various number systems: binary, octal, decimal, and hexadecimal. We will examine the conversions between these systems and provide illustrative examples to enhance our comprehension of this concept.

What is the Number System in Mathematics?

A number system is a defined method of writing and representing numbers. It serves as a mathematical notation that uses consistent symbols or digits to express numbers from a specific set. The number system ensures a distinct representation for each number and reflects the arithmetic and algebraic properties of the figures. Moreover, it enables us to perform fundamental arithmetic operations such as addition, subtraction, multiplication, and division.

The value of a digit within a number can be determined based on three factors:

1. The digit itself
2. The position of the digit within the number
3. The base or radix of the number system being used.

What are Numbers?

Numbers serve mathematical purposes such as counting, measuring, and labelling. They are essential for performing arithmetic calculations. Various types of numbers exist, including natural, whole, rational, and irrational numbers. Additionally, 0 represents a null value. Numbers also exhibit variations like even and odd numbers, as well as prime and composite numbers. The terms "even" and "odd" describe divisibility by 2, while "prime" and "composite" differentiate between numbers with two factors and those with more than two factors, respectively.

In number systems, these numbers function as digits. Binary numbers primarily use the digits 0 and 1. Other number systems utilize the digits 0 to 9. Let's explore the different types of number systems.

Define Number System

A number system refers to the consistent representation of numbers using digits or symbols. The value of a digit within a number depends on the digit itself, its position within the number, and the base of the number system being used. Each number in the system has a distinct representation and enables arithmetic operations such as addition, subtraction, and division.

Number System Chart

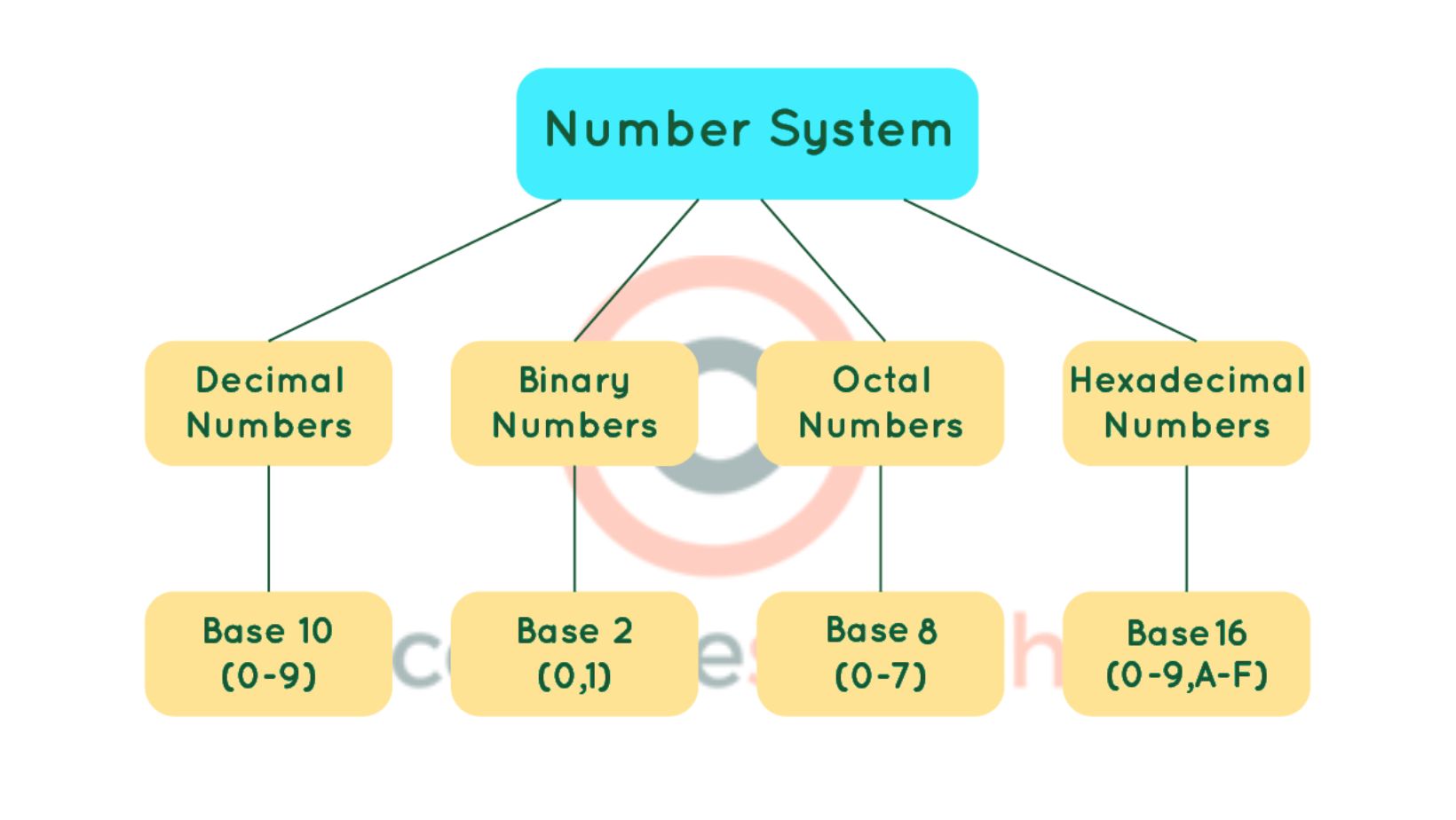
Types of Number System

There are various types of number system. The four main types of number system that we will discuss in brief are:

1. Decimal number system (Base- 10)
2. Binary number system (Base- 2)
3. Octal number system (Base-8)
4. Hexadecimal number system (Base- 16)

Types of Number System: Decimal (Base 10 Number System)

In the decimal number system, the base number is 10, and it employs a set of ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This system is commonly utilized to express numbers in our everyday lives. When a number is presented without specifying its base, it is assumed to be in base 10. For instance, 72310, 3210, and 425710 are a few illustrations of numbers within the decimal number system.

Example of Decimal Number System:

The decimal number 1457 consists of the digit 7 in the units position, 5 in the tens place, 4 in the hundreds position, and 1 in the thousands place whose value can be written as:

(1×103) + (4×102) + (5×101) + (7×100)

(1×1000) + (4×100) + (5×10) + (7×1)

1000 + 400 + 50 + 7

1457

Types of number system: Binary (Base- 2 Number System)

The Binary number system, also referred to as the base 2 number system, utilizes only two digits: 0 and 1. In this system, the base-2 represents a radix of 2. The numbers represented within this system are called binary numbers, consisting exclusively of combinations of 0 and 1. For instance, 110101 is an example of a binary number.

It is possible to convert any number system into binary and vice versa.

For Example:

In the binary system, there are only two digits: 0 and 1. Each digit in a binary number is called a "bit." The position of each bit determines its value, based on powers of 2.

Let's take the binary number 10110. To understand its value, we'll assign powers of 2 to each bit, starting from the rightmost bit:

Calculating the value of each bit:

So, the binary number 10110 is equivalent to the decimal number 22.

Types of Number System: Octal (Base 8 Number System)

The octal numeral system utilizes a base of 8 and consists of eight digits: 0, 1, 2, 3, 4, 5, 6, and 7. One notable advantage of this system is its reduced digit count compared to various other systems, which helps minimize computational errors. The octal system does not include digits such as 8 and 9. Similar to binary, the octal numeral system finds application in minicomputers, employing digits ranging from 0 to 7.

Example:Convert 2158 into a decimal.

Solution:

2158 = 2 × 82 + 1 × 81 + 5 × 80

= 2 × 64 + 1 × 8 + 5 × 1

= 128 + 8 + 5

= 14110

Types of Number System: Hexadecimal (Base 16 Number System)

The hexadecimal number system uses a base of 16 to represent numbers. Initially, numbers in the hexadecimal system are represented similarly to those in the decimal system, ranging from 0 to 9. However, beyond 9, additional symbols from the alphabet, specifically A to F, are used to represent the values. The table below illustrates the representation of numbers in the hexadecimal number system.

Types of Number System Conversion

Numbers can be expressed in various number systems, such as binary, decimal, hexadecimal, and more. It is also possible to convert a number from one system to another with relative ease. To learn the conversion process, refer to the comprehensive lesson on number system conversions. This lesson provides instructions on converting decimal to binary and vice versa, hexadecimal to binary and vice versa, as well as octal to binary and vice versa, accompanied by several examples.

Having covered the different conversion methods described above, let's briefly discuss the conversion from one number system to another using a random number as an example.

Let's consider the number 349. Here is how the number 349 appears in different number systems:

• In the binary system, the number 349 is represented as 101011101.
• In the decimal system, the number 349 remains 349.
• In the octal system, the number 349 is denoted as 535.
• In the hexadecimal system, the number 349 is written as 15D.

Conversion of Binary to Decimal Number System Steps

To convert a number from binary to the decimal system, the following steps are employed:

Step 1:Begin with the rightmost digit of the given binary number and multiply each digit by the corresponding exponent of the base. 

Step 2:The exponents are assigned starting from 0 and incrementing by 1 as we move from right to left. 

Step 3:Simplify the products obtained in the previous step and sum them up.

To illustrate these steps, let's use the following example, where we aim to convert a binary number to the decimal number system.

Example:Convert 1001112 into the decimal system.

Solution:

Step 1:Identify the base of the given number. 

Here, the base of 1001112 is 2.

Step 2: Multiply each digit of the given number, starting from the rightmost digit, with the exponents of the base. The exponents should start with 0 and increase by 1 every time we move from right to left. Since the base is 2, we multiply the digits of the given number by 2⁰, 2¹, 2², and so on from right to left.

Step 3:We just simplify each of the above products and add them.

Here, the sum is the equivalent number in the decimal number system of the given number. or,

We can use the following steps to make this process simplified.

100111 = (1 × 2⁵) + (0 × 2⁴) + (0 × 2³) + (1 × 2²) + (1 × 2¹) + (1 × 2⁰)

= (1 × 32) + (0 × 16) + (0 × 8) + (1 × 4) + (1 × 2) + (1 × 1)

= 32 + 0 + 0 + 4 + 2 + 1

= 39

Thus, 1001112= 3910.

Decimal Number System to Binary / Octal / Hexadecimal Number System Conversion Steps

To convert a number from the decimal system to binary, octal, or hexadecimal, the following steps are utilized. In this instance, we will demonstrate the steps for converting a decimal number to the octal system.

Example:Let's convert the number 432010 to the octal system.

Solution:

Step 1:Determine the base of the target number system. In this case, we are converting to the octal system, so the base is 8.

Step 2: Divide the given number by 8, the base of the octal system. Record the quotient and remainder in the quotient-remainder form. Repeat this process by dividing each subsequent quotient by 8 until we obtain a quotient less than 8.

Step 3:The number in the octal system is obtained by reading the remainders and the last quotient from bottom to top.

Therefore, 432010 = 103408

Steps for Converting One Number System to Another Number System

To convert a number from binary, octal, or hexadecimal systems to another system, the conversion typically involves two steps. First, the number is converted from the original system to the decimal system. Then, the decimal number is converted to the desired system using the respective conversion process.

Example:Let's convert the binary number 10101111002 to the hexadecimal system.

Solution:

Step 1:Convert the given number to the decimal system using the conversion process explained earlier. Thus, 10101111002 = 70010 → (1)

Step 2: Convert the decimal number obtained in step 1 to the hexadecimal system.

In this case, we need to convert 70010 to the hexadecimal system using the provided process. Note that in the hexadecimal system, the numbers 11 and 12 are represented as B and C, respectively. Therefore, 70010 = 2BC16 → (2)

From equations (1) and (2), we conclude that 10101111002 is equal to 2BC16 in the hexadecimal system.

Other Types of Numbers in Number System

There are different types of numbers used in the number system. The table below shows the other types of numbers:

Note: The table lists different number systems and provides examples of numbers within each system. Natural numbers include positive integers, while whole numbers include natural numbers along with zero. Integers consist of both positive and negative whole numbers, including zero. Rational numbers are represented as fractions, and irrational numbers cannot be expressed as fractions and have non-terminating and non-repeating decimal representations.

Computer Number System

In computer systems, the numeral system used is the binary system, which is a base-2 system. The binary system consists of two digits, 0 and 1, and is the fundamental building block for all computer operations. However, computer systems also utilize other numeral systems for convenience and ease of representation. Here are the commonly used numeral systems in computer systems:

• Binary (Base-2): The binary system represents numbers using only two digits, 0 and 1. It is the primary numeral system in computers, as digital circuits can easily represent and manipulate binary values.
• Decimal (Base-10): The decimal system is the most familiar numeral system to humans. It uses ten digits from 0 to 9. Although computers primarily work with binary, decimal numbers are often used for human-readable representation and input/output operations.
• Hexadecimal (Base-16): The hexadecimal system uses sixteen digits, 0-9 and A-F, to represent numbers. It is commonly used in computer systems for compactly representing binary values. Each digit in hexadecimal corresponds to a group of four bits (a nibble) in binary.
• Octal (Base-8): The octal system uses eight digits, 0-7, to represent numbers. It was widely used in early computer systems due to its convenience in representing binary values. However, its usage has decreased with the prevalence of hexadecimal representation.

These different numeral systems allow computers to represent and manipulate data efficiently, depending on the specific requirements of the application or task at hand.

Types of Number System: Things to Remember

1. Whole numbers include all natural numbers, but the reverse is not true.
2. Integers contain natural numbers as a subset.
3. When adding, subtracting, or multiplying two rational numbers, the result is always a rational number.
4. Number systems are used to represent numbers in the computer system.
5. Decimal numbers have a base or radix of 10.
6. Binary numbers are represented using only 0 and 1.
7. Octal numbers have a base value of 8.
8. Hexadecimal numbers have a base value of 16.