Surface Area of a Cone Formula Overview
A three-dimensional form is one that has height or depth. Three-dimensional objects include the sphere, cuboids, cones, and so on. A three-dimensional shape's surface area is the sum of the surface areas of all of its sides. A cone is a three-dimensional shape with a circular base.
What is a Cone?
Cones are circular pyramid-like constructions with a circular base. It has a three-dimensional form with a smooth base that tapers at the highest point, known as the vertex. We assume a right circular cone with a circular base while analyzing the surface area of cones. A cone may be thought of as a triangle that has one of its vertices rotated.

What is the Surface Area?
When determining the surface area of a 3-D object, think about unfolding or flattening the shape and then computing the area of each side. All of these regions are added together to determine the surface area. Square units like square meters, square centimeters, or equivalents are used to measure surface areas. There are two types of surface areas-
- The curved surface area of a cone formula covers only the part that is curved.
- The total surface area of a cone is thesum of the curved surface area and the base circle area.
What is the Surface Area of a Cone?
The surface area of a cone is the area filled by the surface/boundary of a cone. It is usually expressed as a square unit. A cone is formed by stacking multiple triangles and spinning them around one axis. It has a total surface area as well as a curved surface area because it has a flat base. A cone can be classified as either a right circular cone or an oblique cone. In a right circular cone, the vertex is normally vertically above the center of the base, but in an oblique cone, the vertex is not vertically above the center of the base.
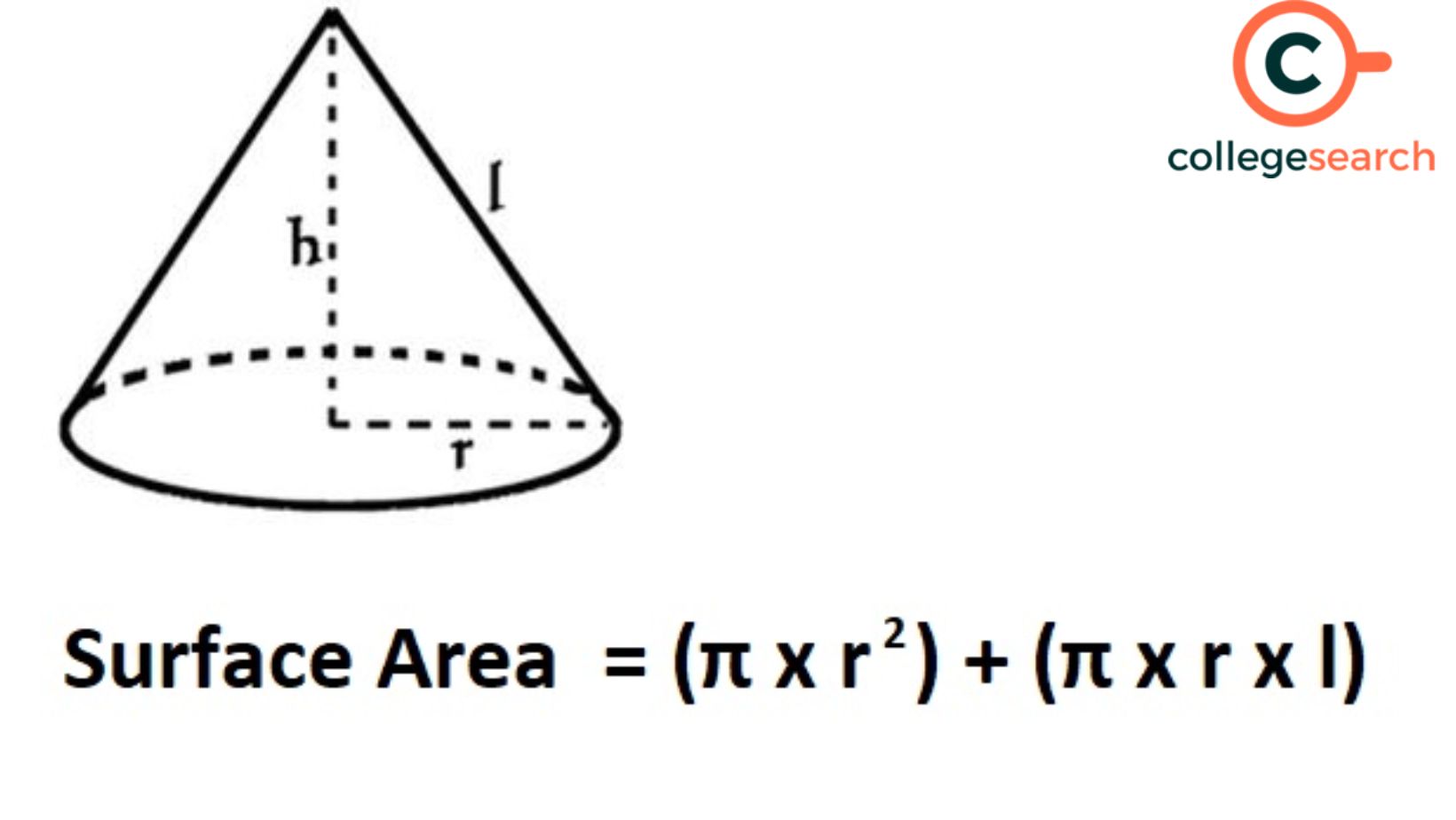
What is the Surface Area of a Cone Formula?
Where r is the radius of the circular base, the circumference of the cone's base equals 2πr. Therefore,
Curved Surface Area of Cone (CSA) = ½ x l x 2πr = πrl
We are aware that a right-angled triangle can be rotated to form a cone. Using the following formula of Pythagoras' Theorem which enables to determine the length of the slant side of a right-angled triangle-
l² = r² + h²
The surface area of the circle = πr²
Area of Curved Surface = πrl
The overall surface area of the cone is equal to the sum of the curved surfaces plus the circumference of the base. Therefore, a cone's total surface area = πr² + πrl
Using r as the common value, we have,
Total Surface area of cone (TSA) = πr (l + r)
Where,
I = Slant height
r = The base circle's radius
SA = Total surface area
h = Height of cone
Read more about the Father of Mathematics.
Surface Area of Cone Formula in terms of Radius and Height
It is also possible to write the CSA formula for a right circular cone as follows-
The radius of a sector with a radius equal to the slant height 'l' is equal to the area of a cone's curved surface. Thus, by Pythagoras' theorem, l² = r² + h²
l = √r² + h²
CSA of Cone = πr√(r² + h²)
Formula for TSA for a Right Circular Cone
The total surface area of a cone formula = the sum of its curved surface area and its circular base area (sector's area).
A cone's total surface area = πr² + πrl
Therefore,
TSA of Cone = πr² + πr√(r² + h²)

Read more about the Maths Formulas.
Derivation of the Surface Area of a Cone Formula
Consider a cone to be a triangle that has one of its vertices rotated. Consider a scenario in which we need to paint the faces of a conical flask. Before we begin painting, we must determine the amount of paint necessary to cover all of the walls. To estimate the amount of paint needed, we need to know the area of each face of the container, which is known as the total surface area. A cone's total surface area is the sum of the areas of its faces. Let's create a universal cone formula to compute a cone's surface area.
